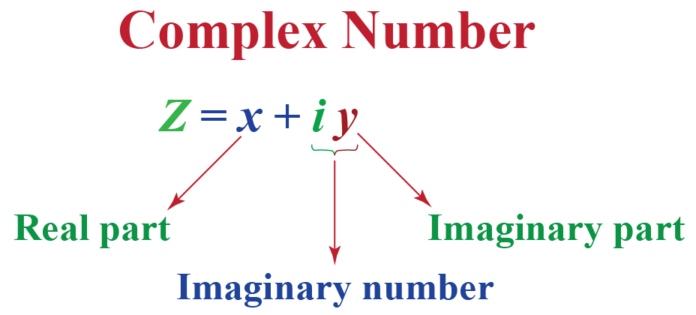In recent times, it has become quite difficult for students to study strategically and earn their desired goals. Not having appropriate guidance is one of the key factors responsible for students lagging in their curriculum. One of the subjects which kids, in general, find difficult and boring is Maths. The concept of Complex numbers is one of the sub-parts of maths that can be quite easy if you know the rules of solving complex numbers. Various online platforms provide guidance and clarity to solve such problems.
Cuemath is an online learning platform that provides classes and worksheets for all your maths queries. It is quite practical and simple to use this website. All the worksheets are separated based on grades and topics, which makes it effortless and a time-saver to find what you are looking for.
What is a complex number?
A complex number is represented as a sum of a real number and an imaginary number. It is represented in the form of ‘a+ib’, where i is the imaginary part, ‘a’ is the real part and is written as Re (z) and, ‘b’ is the imaginary part of the number that is written as Img (z). This number as a whole is represented as ‘z’.
‘i’is called iota and its value is-1. It is valuable in finding the roots of negative numbers. The value of i2= -1 which is also known as the fundamental aspect of a complex number. If you wish to learn more Cuemath online classes are the best and easiest way to do so under the guidance of expert teachers.
Modulus of a complex number:
The modulus of a complex number is the square root of the sum of the square of the real and imaginary part of the complex number. It is represented as
z= a2+b2 . In other terms, it is represented as the distance of a complex number represented as a point in the argand plane i.e. the distance from the point (0,0) to the point (a, ib).
The argument of a complex number:
The argument of a complex number is defined as the angle formed by the line joining the origin with the point (a, ib) and the positive x-axis. It is known as Θ that is the inverse of tan of the imaginary part divided by the real part. It is represented asArgz= ba .
Polar representation of a complex number:
With the modulus and argument of a complex number, it can be represented in the polar formz=rθ +isin ) , which is also written as rcisΘ, where r is the modulus of a complex number and Θ is the argument of the complex number that is represented as=ba .
The polar coordinates of a complex number are (r, Θ) and (r, Θ+2KΠ), K being an integer. Therefore, the polar representation of a complex number is not unique.
Operations on a complex number:
#1. Addition:
- The addition of a complex number is quite simple and similar to the addition of integers.
- While adding two complex numbers i.e. Z1+Z2, the real parts are added together and the imaginary parts are added together.
- Considering,
z1=(a+ib), z2=c+id, z1+z2=a+c+i(b+d)
#2. Subtraction:
- The subtraction of a complex number is performed in the same way as the addition.
- When subtracting two complex numbers, the real parts are subtracted together and the imaginary parts are subtracted together.
- Considering,
z1=a+ib, z2=c+id, z1–z2=a-c+i(b-d)
#3. Multiplication:
- It is different from the multiplication of integers. Since it involves the term iota, therefore, the multiplication of two complex numbers gives us the term i2= -1.
- Considering,
z1=a+ib, z2=c+id,z1z2=ac-bd+i(ad+bc)
- Multiplication in polar form is different from the above method.
- If z1=r1(cos 1+i sin 1), z2=r2cos 2 +isin θ 2,
z1z2=r1r2(cos (θ1+2)+i sin (θ1+2))
#4. Division:
- Division of a complex number is performed with the property of reciprocal of a complex number.
- Considering,
z1=a+ib, z2=c+id, z1z2=a+ib*(c-id)(c2+d2)
The above mentioned are the most basic and important things to know about complex numbers.